flowchart LR
A(A cat does cat things) --> B{" "}
B --> C(A)
B --> D(cat)
B --> E(does)
B --> F(cat)
B --> G(things)
D --> H(cat)
E --> I(do)
F --> J(cat)
G --> K(thing)
H --> L(cat: 2)
J --> L
I --> M(do: 1)
K --> N(thing: 1)
L --> O(2)
M --> P(1)
N --> Q(1)
Large Language Models: An ‘intuitive’ introduction
Background
- Rise of machine learning and deep learning in the 2000s
- Idea: Use neural networks for NLP tasks
- Challenge: How do we feed text into a neural network?
Answer: Text embeddings!
Example from Bag of Words
How could a neural network look like?
flowchart LR A(Input Text) --> B(Tokenization) B --> C(Token processing) C --> D(Embedding Layer) D --> E(Hidden Layers) E --> F(Output Layer)
- The hidden layers and output layers depend on the application
- The rest of the layers can be pre-trained (later)
Example: Text classification
flowchart LR A(Input Text) --> B(Tokenization) B --> C(Token processing) C --> D(Embedding Layer) D --> E(Hidden Layers) E --> F(Output Layer)
- Classifying news articles into categories (sports, politics, …)
- Training data: Dataset with corresponding category or label
- Data processing: Tokenization, stop words, lower casing etc.
- Training:
- Measure the difference between predicted and true labels and adjust network weights
- Example: BoW embeddings - frequency of words affects label likelihood.
Sequence Generation and Language Modeling
Sequence generation
- Idea: Models are trained to generate sequences of data (mostly: text) based on input/context.
- Sequences have to resemble the training data.
- Application: Text generation, music composition, image captioning
- Requires understanding language structure for meaningful output!
Language modeling
Idea: Train a model to predict the probability distribution of words or tokens in a sequence given the preceding context!
flowchart LR
A(The) --> B(bird)
B --> C(flew)
C --> D(over)
D --> E(the)
E --> F{?}
F --> G("p(rooftops)=0.31")
F --> H("p(trees)=0.14")
F --> J("p(guitar)=0.001")
Training Process
- Expose the model to large text datasets (great: we have the internet!)
- Teach the model statistical properties of language (Which token comes next?)
- Capture syntactic structures, semantic relationships, and contextual nuances
- Training happens in an unsupervised fashion (we require no labels!)
Challenges
- Handling vast and diverse nature of human language.
- Complex patterns, variations, and ambiguities.
- Out-of-vocabulary words, long-range dependencies, domain-specific knowledge.
- Requires robust architectures and sophisticated algorithms.
BUT: They did it and it works!
GPT: Generative Pre-trained Transformer
What is GPT?
- current state-of-the-art language model
- introduced in the paper “Attention is All You Need” by Vaswani et al. in 2017 (Google)
- GPT belongs to the family of transformer-based models
- key advantage over previous approaches:
- self-attention
- scalability
What is a transformer?
- Traditional approach:
- information flow constrained by fixed-length context windows or recurrent connections
- One token at a time (in RNNs)
- New approach:
- Each word in a sentence can attend to all other words simultaneously (self-attention)
- Dynamically weigh the importance of each word in the context of the entire sequence
- Semantically related words receive higher attention weights
- Irrelevant or less informative words receive lower weights
- Processing all sequences in parallel
A deeper dive: What an LLM wants to do!
flowchart LR A(Token 1) B(Token 2) C(Token 3) D(...) E(Token k) F(The core of the LLM) A --> F B --> F C --> F D --> F E --> F AA(Prob. dist. 1st output token) BB(Prob. dist. 2nd output token) CC(...) DD(Prob. dist. nth output token) F --> AA F --> BB F --> CC F --> DD
How can we generate a probability distribution?
Idea: Transform a vector \(z\) of numbers into a probability distribution!
\[ \text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}} \]
Softmax input z: [2.0, 1.0, 0.1, -1.0, 2.0]
Softmax output: [0.39, 0.14, 0.06, 0.02, 0.39]
Great, so let’s try to generate vectors with our model!
A deeper dive: What an LLM looks like!
flowchart LR A(Input Text) --> B(Tokenization) --> C(Token Embedding) -.-> X:::hidden Y:::hidden -.-> D(Attention) --> E(Multilayer Perceptron) --> F(Attention) --> G(Multilayer Perceptron) --> H(...) -.-> Z:::hidden XX:::hidden -.-> I(Unembedding) --> J(Probabilities) --> K(Token Output)
General idea: Transform input vectors (embeddings) over and over such that the result encodes all the context!
Token embeddings
Tokenization:
flowchart LR A(A) --> B(blue) --> C(guitar) --> D(is) --> E(?)
Embedding:
\[W_E = \begin{bmatrix} 0.25 & -0.73 & 0.58 & 0.44 \\ -0.53 & 0.57 & -0.61 & 0.70 \\ 0.11 & 0.33 & 0.22 & -0.49 \\ -0.80 & -0.08 & -0.73 & 0.29 \\ \end{bmatrix} \]
Token embeddings
- One embedding \(E_k\) per token (lookup table, but it’s being learned during training!)
- No connection (“context”) between token embeddings at first
- But: Directional information contained in embeddings which encodes “meaning”
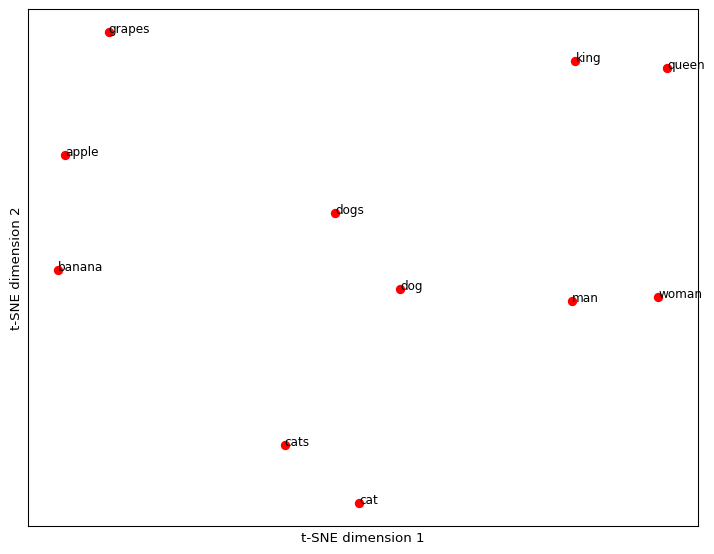
Embedding visualization
Unembedding, probabilities and token output
What happens at the end of the LLM?
flowchart LR
A(A) --> AA("$$E_1$$")
B(blue) --> BB("$$E_2$$")
C(guitar) --> CC("$$E_3$$")
D(is) --> DD("$$E_4$$")
E(The core of the LLM)
AA --> E
BB --> E
CC --> E
DD --> E
F(Unembedding matrix)
E --> F
AAA("$$U_1$$")
BBB("$$U_2$$")
CCC("$$U_3$$")
F --> AAA
F --> BBB
F --> CCC
G(Softmax) --> GG(Prob. dist. 1st output token)
H(Softmax) --> HH(Prob. dist. 2nd output token)
I(Softmax) --> II(Prob. dist 3rd output token)
AAA --> G
BBB --> H
CCC --> I
GG --> X("p(great)=0.31")
GG --> Y("p(aweful)=0.14")
GG --> Z("p(train)=0.001")
Understanding the core: Attention
- Problem: Embedding vectors so far do not interact with each other, so we cannot process “context”.
- Solution: Let embedding vectors \(E_k\) share information!
flowchart LR
A("$$E_1^{(1)}$$")
B("$$E_2^{(1)}$$")
C("$$E_3^{(1)}$$")
D("$$E_k^{(1)}$$")
E("Transformation ('Attention')")
A --> E
B --> E
C --> E
D --> E
F("$$E_1^{(2)}$$")
G("$$E_2^{(2)}$$")
H("$$E_3^{(2)}$$")
I("$$E_k^{(2)}$$")
E --> F
E --> G
E --> H
E --> I
–
Understanding the core: Attention
\[ \text{Attention}(Q, K, V) = \text{softmax}(K^T Q)V \]
- \(Q\) is the “query”, asking a question
- \(K\) is the “key”, answering that question
- \(\text{softmax}\) turns the result into a weight (“How important is that question and its answer?”)
- Then we multiply with the value matrix \(V\) that transforms the initial embedding vectors, that now encode shared information!
Understanding the core: Attention
\[ \text{Attention}(Q, K, V) = \text{softmax}(K^T Q)V \]
\[K_i = E_i * W_K\] \[Q_i = E_i * W_Q\]
\[ \text{softmax}( \begin{bmatrix} K_1 \cdot Q_1 & K_1 \cdot Q_2 & K_1 \cdot Q_3 \\ K_2 \cdot Q_1 & K_2 \cdot Q_2 & K_2 \cdot Q_3 \\ K_3 \cdot Q_1 & K_3 \cdot Q_2 & K_3 \cdot Q_3 \end{bmatrix}) V \]
Multilayer Perceptron
- A “standard” neural network which works in the same way that other work.
- Can be thought of as “more parameters to tune in the network”!
- Won’t go into details here.
Put it all together
flowchart LR
A(A) --> AA("$$E_1$$")
B(blue) --> BB("$$E_2$$")
C(guitar) --> CC("$$E_3$$")
D(is) --> DD("$$E_4$$")
E(Attention and MP)
AA --> E
BB --> E
CC --> E
DD --> E
REP(Repeat 10k times)
F(Unembedding matrix)
E --> REP
REP --> F
AAA("$$U_1$$")
BBB("$$U_2$$")
CCC("$$U_3$$")
F --> AAA
F --> BBB
F --> CCC
G(Softmax) --> GG(Prob. dist. 1st output token)
H(Softmax) --> HH(Prob. dist. 2nd output token)
I(Softmax) --> II(Prob. dist 3rd output token)
AAA --> G
BBB --> H
CCC --> I
GG --> X("p(great)=0.31")
GG --> Y("p(aweful)=0.14")
GG --> Z("p(train)=0.001")
We have created a machine that can generate the most likely next token!
There are some details that need consideration
- Details of the Multilayer Perceptron layers
- Training of an LLM involves a second step (reinforcement learning)
- Sampling, temperature scaling, \(\text{top_}{p}\) (How can an LLM be creative?)
- How does the memory of an LLM work?
- Many, many details we skipped!
But for now, let’s get started using one!
Seminar: LLM, SoSe 2025